👀 본 예제는 Window10의 VSCode, Python3.11.0로 작성되었습니다.
영상의 기하학적(Geometric Transform)은 영상을 구성하는 픽셀의 배치 구조를 변경함으로써 전체 영상의 모양을 바꾸는 작업이다.
이전 필터링은 픽셀의 위치를 고정하고 픽셀의 값을 변경하였지만 기하학적 변환은 픽셀 값은 그대로 유지하면서 위치를 변경하는 작업이다.
Affine Transform
영상을 평행 이동시키거나 회전, 크기 변환 등을 통해 만들 수 있는 변환을 통칭한다.
Affine 변환의 경우 직선 간의 길이 비율과 평행 관계가 그대로 유지된다.
# transforms.py
import cv2
import numpy as np
def affineTransform(image:np.ndarray,matrix:np.ndarray,shape:tuple):
return cv2.warpAffine(image,matrix,shape)
# main.py
import cv2
import numpy as np
# affine
from transforms import affineTransform
def show(origin:np.ndarray,result:np.ndarray):
cv2.imshow("origin",origin)
cv2.imshow("result",result)
cv2.waitKey(0)
cv2.destroyAllWindows()
img = cv2.imread("test.png")
img = cv2.resize(img,(480,480))
points_src = np.float32([[50, 50], [200, 50], [50, 200]]) # 변환 전의 점들
points_dst = np.float32([[10, 100], [200, 50], [100, 250]]) # 변환 후의 점들
matrix = cv2.getAffineTransform(points_src,points_dst)
aff_result = affineTransform(img,matrix,img.shape[:2])
show(img,aff_result)
Translation Transformation
이동 변환은 영상을 가로 또는 세로 방향으로 일정 크기만큼 이동시키는 연산(시프트 연산)을 의미한다.
# transforms.py
import cv2
import numpy as np
def translationTransform(image:np.ndarray,matrix:np.ndarray,shape:tuple):
return cv2.warpAffine(image,matrix,shape)
# main.py
import cv2
import numpy as np
# affine
from transforms import affineTransform
def show(origin:np.ndarray,result:np.ndarray):
cv2.imshow("origin",origin)
cv2.imshow("result",result)
cv2.waitKey(0)
cv2.destroyAllWindows()
img = cv2.imread("test.png")
img = cv2.resize(img,(480,480))
tx = 100 # x축으로 이동할 거리
ty = 50 # y축으로 이동할 거리
matrix = np.float32([[1,0,tx],[0,1,ty]])
result = translationTransform(img,matrix,img.shape[:2])
show(img,result)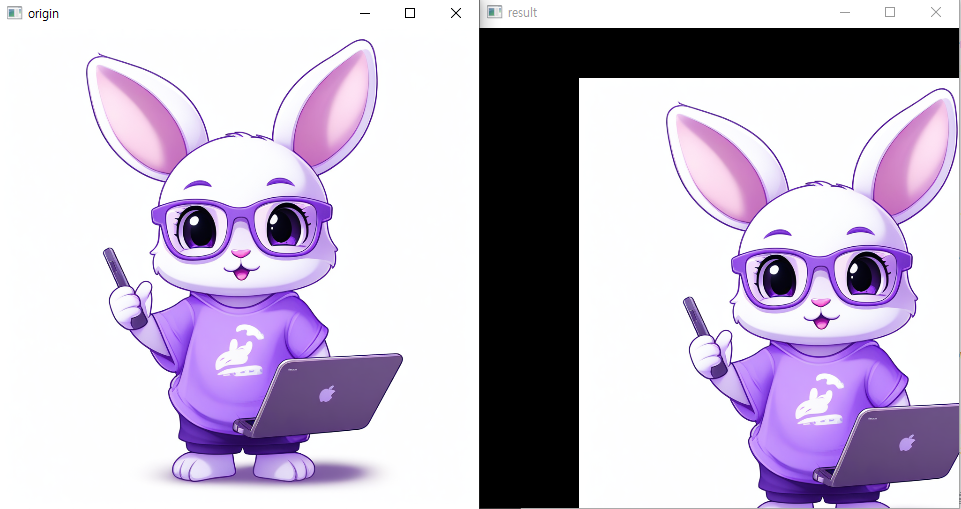
Shear Transformation
전단 변환은 직사각형 형태의 영상을 한쪽 방향을 밀어서 평행사변형 모양으로 변형되는 변환이며 층밀림 변환이라고도 한다.
# transforms.py
import cv2
import numpy as np
def transformation(image:np.ndarray,matrix:np.ndarray,shape:tuple):
return cv2.warpAffine(image,matrix,shape)
# main.py
import cv2
import numpy as np
# affine
from transforms import transformation
def show(origin:np.ndarray,result:np.ndarray):
cv2.imshow("origin",origin)
cv2.imshow("result",result)
cv2.waitKey(0)
cv2.destroyAllWindows()
img = cv2.imread("test.png")
img = cv2.resize(img,(480,480))
shear_factor = 0.5
matrix = np.float32([[1, shear_factor, 0], [0, 1, 0]])
shape = img.shape[:2]
result = transformation(img,matrix,(int(shape[0]+shape[1] * shear_factor),shape[1]))
show(img,result)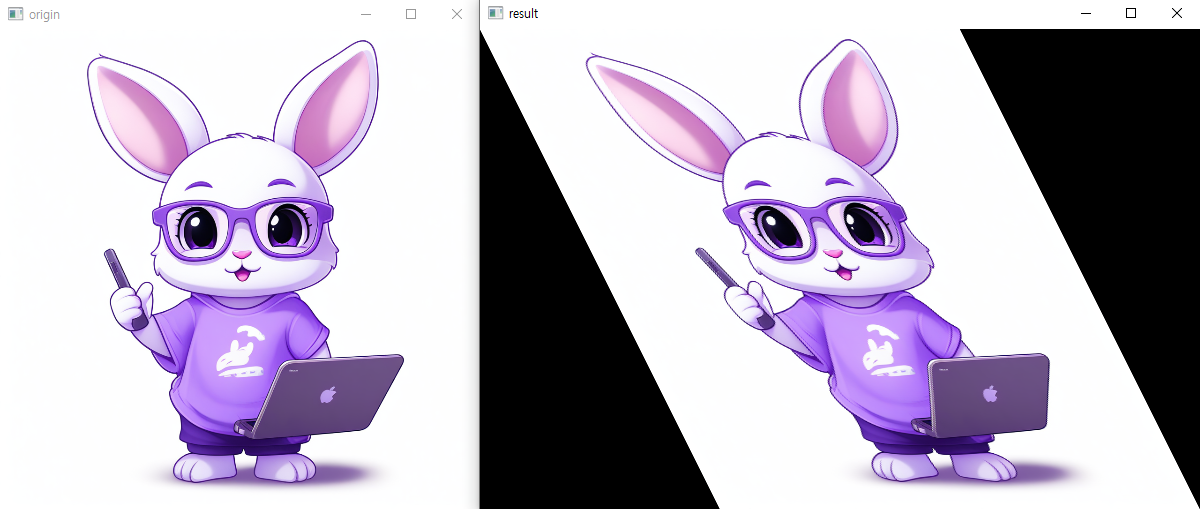
Scale Transformation
영상의 크기 변환은 영상의 전체적인 크기를 확대 또는 축소하는 변환이다.
영상의 스케일링 시 영상 손실이 있기 때문에 그때에 맞는 보간법으로 영상 손실을 최소화 해야한다.
InterpolationFlags
- cv2.INTER_NEAREST : 가장 간단, 가장 가까운 픽셀 값을 사용
- cv2. INTER_LINEAR : 2x2 픽셀 네트워크에서 선형 보간 수행, 일반적인 확대 및 축소에 적합
- cv2. INTER_CUBIC : 4x4 픽셀 네트워크에서 3차 보간 사용, 확대할 때 주로 사용
- cv2. INTER_AREA : 픽셀 영역 평균을 사용하여 이미지를 축소할 때 주로 사용, 축소 시 품질 좋고, 모자이크 효과를 줄이는 데 효과적
- cv2. INTER_LANCZOS4 : 8x8 픽셀 네트워크에서 Lanczos 재샘플링을 사용, 가장 성능이 좋고 축소시 때 효과적
import cv2
import numpy as np
def show(origin:np.ndarray,result:np.ndarray):
cv2.imshow("origin",origin)
cv2.imshow("result",result)
cv2.waitKey(0)
cv2.destroyAllWindows()
img = cv2.imread("test.png")
img = cv2.resize(img,(480,480))
result = cv2.resize(img,None,fx=1.5,fy=1.5,interpolation=cv2.INTER_LANCZOS4)
show(img,result)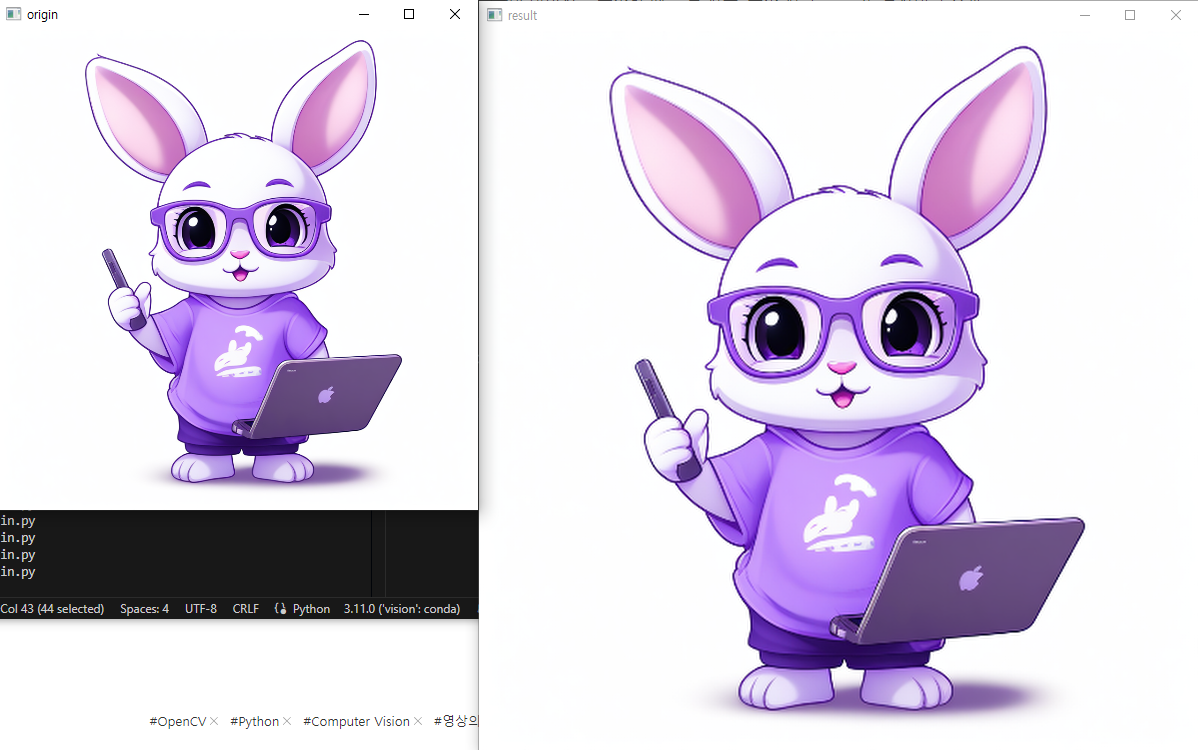
Rotation Transformation
영상 처리 시스템을 만들다보면 영상을 회전 시켜야할 때가 종종 발생한다.
이때 사용하는 회전 변환은 특정 좌표를 기준으로 영상을 원하는 각도만큼 회전하는 변환이다.
import cv2
import numpy as np
# affine
from transforms import transformation
def show(origin:np.ndarray,result:np.ndarray):
cv2.imshow("origin",origin)
cv2.imshow("result",result)
cv2.waitKey(0)
cv2.destroyAllWindows()
img = cv2.imread("test.png")
img = cv2.resize(img,(480,480))
# 회전 축 좌표
h,w,_ = img.shape
center = (h // 2,w // 2)
# 회전 각도
angle = 45
# 변호나 행렬
matrix = cv2.getRotationMatrix2D(center,angle,1.0) # 마지막 인자는 스케일링
result = transformation(img,matrix,(w,h))
show(img,result)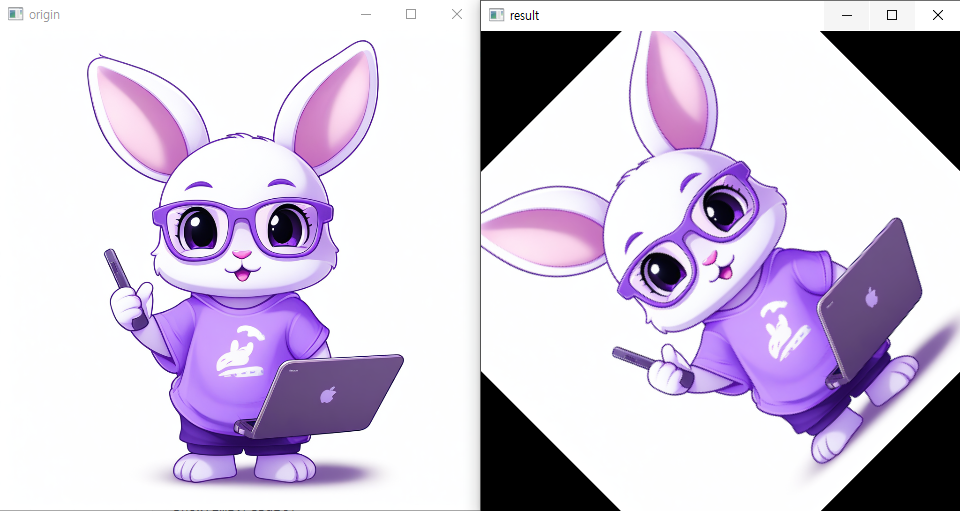
Symmetry Transformation
대칭 변환은 영상을 마치 거울에 비친 것처럼 좌우를 바꾸는 변환을 좌우 대칭 또는 좌우 반전이라고 한다.
입력 영상과 출력 영상이 일대일 대응되므로 보간법이 필요하지 않는다.
import cv2
import numpy as np
def show(origin:np.ndarray,result:np.ndarray):
cv2.imshow("origin",origin)
cv2.imshow("result",result)
cv2.waitKey(0)
cv2.destroyAllWindows()
img = cv2.imread("test.png")
img = cv2.resize(img,(480,480))
cv2.imshow("origin",origin)
# 수평 대칭 (X축 기준)
horizontal_flip = cv2.flip(img, 0)
cv2.imshow("horizon",horizontal_flip)
# 수직 대칭 (Y축 기준)
vertical_flip = cv2.flip(img, 1)
cv2.imshow("vertical",vertical_flip)
# 중심 대칭 (원점 기준)
both_flip = cv2.flip(img, -1)
cv2.imshow("both",both_flip)
cv2.waitKey(0)
cv2.destroyAllWindows()
Perspectuve Transform
투시 변환은 직사각형 형태의 영상을 임의의 볼록 사각형 형태로 변경할 수 있는 변환이다.
투시 변환에 의해 원본 영상에 있던 직선은 결과 영상에서 그대로 직선성이 유지되지만, 두 직선의 평행 관계는 깨어질 수 있다.
import cv2
import numpy as np
# affine
from transforms import transformation_per
def show(origin:np.ndarray,result:np.ndarray):
cv2.imshow("origin",origin)
cv2.imshow("result",result)
cv2.waitKey(0)
cv2.destroyAllWindows()
img = cv2.imread("test.png")
img = cv2.resize(img,(480,480))
# 원본 이미지에서 변환할 네 점 (시작점)
points = np.float32([[50, 50], [200, 50], [50, 200], [200, 200]])
# 변환할 네 점 (대상점)
dst_points = np.float32([[10, 10], [300, 50], [50, 250], [250, 200]])
# 투시 변환 행렬 생성
matrix = cv2.getPerspectiveTransform(points, dst_points)
# 이미지에 투시 변환 적용
height, width = img.shape[:2]
result = cv2.warpPerspective(img, matrix, (width, height))
show(img,result)
'AI > Computer Vision' 카테고리의 다른 글
| [Computer Vision] 컬러 영상 처리 (0) | 2024.09.02 |
|---|---|
| [Computer Vision] 에지(Edge) 검출 (0) | 2024.09.02 |
| [Computer Vision] Filtering (0) | 2024.08.30 |
| [Computer Vision] 영상의 명암 제어 (0) | 2024.08.28 |
| [Computer Vision] 텍스트 삽입 및 유용한 기능 (0) | 2024.08.28 |



