SVM(Support Vector Machine)이란?
SVM은 선형이나 비선형 분류, 회귀, 이상치 탐색 등에 사용 가능한 다목적 머신러닝 모델이다.
- 분류에 적용
- 라지 마진 분류(Large Margin Classification)에 해당한다.
- 클래스를 구분 짓는 가장 폭이 넓은 도로 찾기
- 서포트 벡터(Support Vector) : 도로 경계(결정 경계)에 위치한 샘플
- ex. 붓꽃 데이터의 분류
- 라지 마진 분류(Large Margin Classification)에 해당한다.

- 특성 스케일에 민감하다.
- 특성 스케일링을 통해 더 나은 결정 경계(SV) 생성이 가능하다.
- ex. 스케일링에 따른 결정 경계 차이

비선형 SVM 분류 - 하드 마진 분류
모든 샘플이 경계(Support Vector) 밖에 분류 되어야 한다.
- 마진 오류 = 0
이상치에 민감하다.
- 서포트 벡터를 찾지 못할 수도 있다.
ex. 붓꽃 데이터에 이상치 값을 추가한 경우

비선형 SVM 분류 - 소프트 마진 분류
일부 샘플이 경계(Support Vector) 안쪽이나 반대쪽에 있는 것을 허용한다.
- 마진 오류 > 0
마진 오류가 있지만, 더 일반화되는 효과가 있다.
사이킷런의 SVM 모델의 하이퍼파라미터 "C"의 값을 통해 마진 오류 정도를 조절 가능하다.
ex. 붓꽃 데이터의 C 조정

SVM 분류 모델 예시 : LinearSVC
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
X = iris['data'][:,(2,3)] # 꽃잎의 길이, 꽃잎 너비
y = (iris['target'] == 2).astype(np.float64) # iris virginica
# 머신러닝 모델 학습을 위한 파이프라인 작성
# 데이터를 특성 스케일링 후 LinearSVC에 전달한다.
# LinearSVC는 손실함수 "힌지손실함수", 마진 오류 1
svm_clf = Pipeline([
("scler",StandardScaler()),
("linear_svc",LinearSVC(C=1, loss="hinge",random_state=42)),
])
svm_clf.fit(X,y)
비선형 SVM 분류 - 다항 특성 추가
기존 특성으로 선형 분류가 불가능하다면, 다항 특성을 추가하여 분류한다.
예시 - 그림

예시 - moons 데이터셋의 비선형 분류
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
X,y = make_moons(n_samples=100,noise=0.15,random_state=42)
def plot_dataset(X,y,axes):
plt.plot(X[:, 0][y==0], X[:, 1][y==0],'bs')
plt.plot(X[:, 0][y==1], X[:, 1][y==1],'g^')
plt.axis(axes)
plt.grid(True,which='both')
plt.xlabel(r'X1',fontsize=20)
plt.ylabel(r'X2',fontsize=20,rotation=0)
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.show()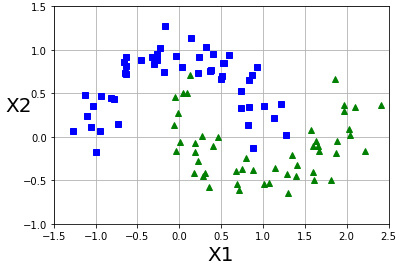
import numpy as np
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
polynomial_svm_clf = Pipeline([
("poly_features",PolynomialFeatures(degree=3)),
("scaler",StandardScaler()),
("svm_clf",LinearSVC(C=10,loss="hinge",random_state=42)),
])
polynomial_svm_clf.fit(X,y)
def plot_predict(clf,axes):
x0s = np.linspace(axes[0],axes[1],100)
x1s = np.linspace(axes[0],axes[3],100)
x0,x1 = np.meshgrid(x0s,x1s)
X = np.c_[x0.ravel(),x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contour(x0,x1,y_pred,cmap=plt.cm.brg,alpha=0.2)
plt.contour(x0,x1,y_decision,cmap=plt.cm.brg,alpha=0.1)
plot_predict(polynomial_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.show()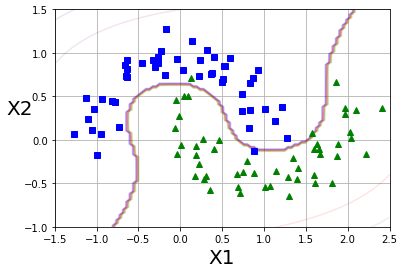
비선형 SVM 분류 - 다항식 커널
다항식 특성 추가의 적절한 차수 찾기
- 낮은 차수 - 복잡한 데이터셋을 잘 표현하지 못한다.
- 높은 차수 - 굉장히 많은 특성이 추가돼 모델의 속도를 저하시킨다.
다항식 커널 트릭(kernel trick)
- 실제로 특성을 추가하지 않으면서, 다항식 특성 추가와 같은 결과를 만드는 수학적 기교이다.
- 사이킷런의 SVC 모델에서의 하이퍼파라미터 kernel='poly',degree 제공(LinearSVC는 커널 트릭 미제공)
- d : degree(최고차 항)
- r : 차수에 영향을 받는 정도
- C : 마진 오류 정도
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
('scaler',StandardScaler()),
('svm_clf',SVC(kernel='poly',degree=3,coef0=1,C=5))
])
poly_kernel_svm_clf.fit(X,y)
poly100_kernel_svm_clf = Pipeline([
('scaler',StandardScaler()),
('svm_clf',SVC(kernel='poly',degree=3,coef0=100,C=5))
])
poly100_kernel_svm_clf.fit(X,y)
plt.figure(figsize=(11,4))
plt.subplot(121)
# 위에서 정의했던 plot 그리는 함수
plot_predict(poly_kernel_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.title(r'd=3,r=1,C=5',fontsize=18)
plt.subplot(122)
# 위에서 정의했던 plot 그리는 함수
plot_predict(poly100_kernel_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.title(r'd=10,r=100,C=5',fontsize=18)
plt.show()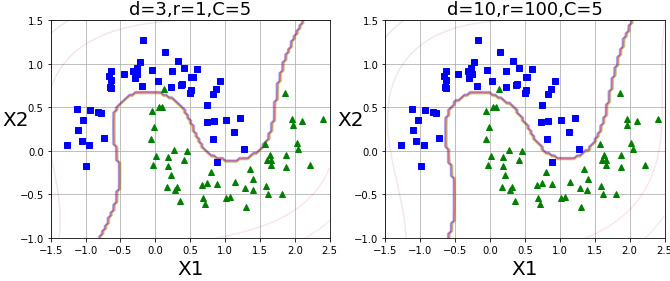
비선형 SVM 분류 - 유사도 특성 추가
- 유사도 특성 추가
- 기존 특성들을 가지고 유사도 특성을 추가한다.
- 유사도 특성 : 각 샘플이 특정 랜드마크(landmark)와 얼마나 닮았는지 측정한 값이다.
- 랜드마크 설정 : 모든 샘플 위치에 랜드마크 설정, 즉 m개 샘플이면 m x m 특성 생성
- 유사도 함수(similarity function) : 유사도를 계산하는 함수이다.
- 유사도 함수 예 : 가우시안 RBF(방사 기저 함수, radial basis function)
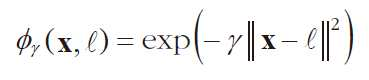
- 예시, 유사도 특성 x2(랜드마크-2), x3(랜드마크 1)을 이용한 SVM 분류
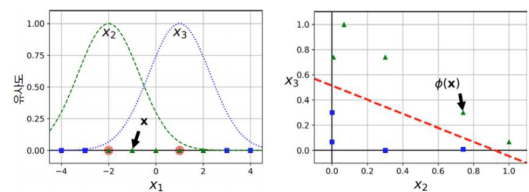
비선형 SVM 분류 - 가우시안 RBF 커널
실제로 특성을 추가하지 않으면서, 유사도 특성 추가와 같은 결과를 만드는 수학적 기교이다.
사이킷런의 SVC 모델에서의 하이퍼파라미터 kernel='rbf', gamma 제공
예
gamma1,gamma2 = 0.1,5
C1,C2 = 0.001,1000
hyperparams = (gamma1,C1),(gamma1,C2),(gamma2,C1),(gamma2,C2)
svm_clfs = []
for gamma,C in hyperparams:
rbf_kernel_svm_clf = Pipeline([
('scaler',StandardScaler()),
('svm_clf',SVC(kernel='rbf',gamma=gamma,C=C))
])
rbf_kernel_svm_clf.fit(X,y)
svm_clfs.append(rbf_kernel_svm_clf)
plt.figure(figsize=(11,7))
for i,svm_clf in enumerate(svm_clfs):
plt.subplots_adjust(left=0.125, bottom=0.1, right=0.9, top=0.9, wspace=0.2, hspace=0.35)
plt.subplot(221+i)
plot_predict(svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
gamma,C = hyperparams[i]
plt.title(r'γ = {0},C = {1}'.format(gamma,C),fontsize=16)
plt.show()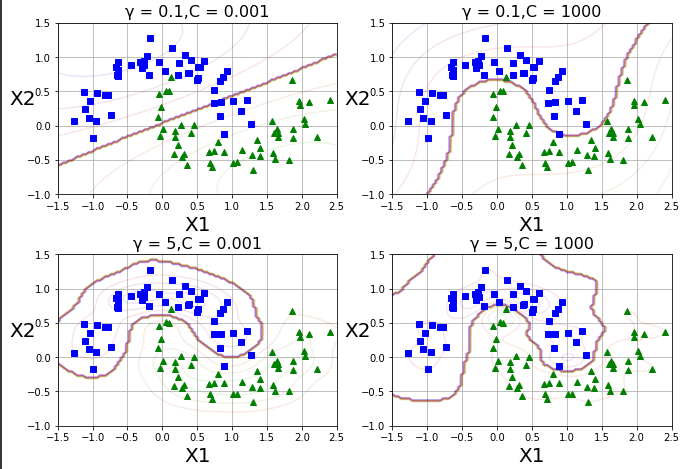
SVM 회귀
SVM을 분류가 아니라 회귀에 적용하는 방법이다.
목표를 반대로 하는 것 - 서포트 벡터 안쪽에 가능한 많은 샘플이 들어가도록 하는 것 이다.
SVM 회귀 - 선형 SVM 회귀
서포트 벡터의 폭은 하이퍼파라미터 ε(epsilon)으로 조절한다.
사이킷런의 선형 SVM 회귀 모델 : LinearSVR
예
np.random.seed(42)
m = 50
X = 2 * np.random.rand(m,1)
y = (4+3*X+np.random.randn(m,1)).ravel()
from sklearn.svm import LinearSVR
svm_reg1 = LinearSVR(epsilon=1.5,random_state=42)
svm_reg1.fit(X,y)
svm_reg2 = LinearSVR(epsilon=0.5,random_state=42)
svm_reg2.fit(X,y)
def find_SV(svm_reg,X,y):
y_pred = svm_reg.predict(X)
off_margin = (np.abs(y-y_pred)>= svm_reg.epsilon)
return np.argwhere(off_margin)
svm_reg1.support_ = find_SV(svm_reg1,X,y)
svm_reg2.support_ = find_SV(svm_reg2,X,y)
eps_x1 = 1
eps_y_pred = svm_reg1.predict([[eps_x1]])
def plot_svm_regression(svm_reg,X,y,axes):
x1s = np.linspace(axes[0],axes[1],100).reshape(100,1)
y_pred = svm_reg.predict(x1s)
plt.plot(x1s,y_pred,'k-',linewidth=2,label=r'y^')
plt.plot(x1s,y_pred + svm_reg.epsilon,'k--')
plt.plot(x1s,y_pred - svm_reg.epsilon,'k--')
plt.scatter(X[svm_reg.support_],y[svm_reg.support_],s=180,facecolors='#FFAAAA')
plt.plot(X,y,'bo')
plt.xlabel(r'X1',fontsize=18)
plt.legend(loc='upper left',fontsize=18)
plt.axis(axes)
plt.figure(figsize=(9,4))
plt.subplot(121)
plot_svm_regression(svm_reg1,X,y,[0,2,3,11])
plt.title(r'epsilon = {0}'.format(svm_reg1.epsilon),fontsize=18)
plt.ylabel(r'y',fontsize=18,rotation=0)
plt.annotate(
'',xy= (eps_x1,eps_y_pred),xycoords='data',
xytext = (eps_x1,eps_y_pred-svm_reg1.epsilon),
textcoords= 'data',arrowprops={'arrowstyle':'<->','linewidth':1.5}
)
plt.text(0.91,5.6,r'epsilon',fontsize=20)
plt.subplot(122)
plot_svm_regression(svm_reg2,X,y,[0,2,3,11])
plt.title(r"epsilon = {0}".format(svm_reg2.epsilon),fontsize=18)
plt.show()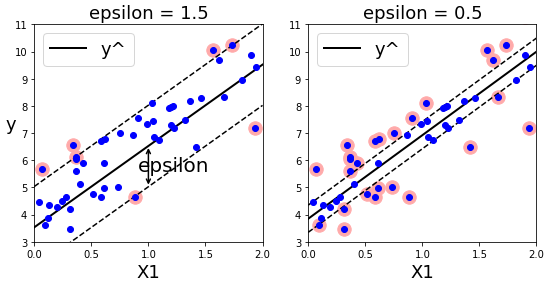
SVM 회귀 - 비선형 SVM 회귀
다항 특성을 추가하거나 커널 트릭을 이용한다.사이킷런의 비선형 SVM 회귀 모델 : SVR
예
np.random.seed(42)
m = 100
X = 2*np.random.rand(m,1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + np.random.randn(m,1)/10).ravel()
from sklearn.svm import SVR
svm_poly_reg1 = SVR(kernel='poly',gamma='auto',degree=2,C=100,epsilon=0.1)
svm_poly_reg2 = SVR(kernel='poly',gamma='auto',degree=2,C=0.01,epsilon=0.1)
svm_poly_reg1.fit(X,y)
svm_poly_reg2.fit(X,y)
plt.figure(figsize=(9,4))
plt.subplot(121)
plot_svm_regression(svm_poly_reg1,X,y,[-1,1,0,1])
plt.title(r'degree = {0},C = {1}, epsilon = {2}'.format(svm_poly_reg1.degree,svm_poly_reg1.C,svm_poly_reg1.epsilon))
plt.ylabel(r'y',fontsize=18,rotation=0)
plt.subplot(122)
plot_svm_regression(svm_poly_reg2,X,y,[-1,1,0,1])
plt.title(r'degree = {0},C = {1}, epsilon = {2}'.format(svm_poly_reg2.degree,svm_poly_reg2.C,svm_poly_reg2.epsilon))
plt.ylabel(r'y',fontsize=18,rotation=0)
plt.show()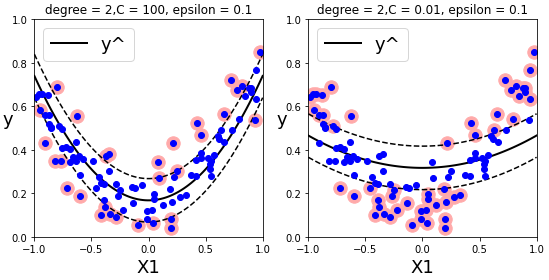
'AI > 기계학습(Machine Learning)' 카테고리의 다른 글
| [기계학습/ML]15. 비지도학습 - 주성분 분석 (0) | 2022.12.05 |
|---|---|
| [기계학습/ML]14. 비지도학습 - K-평균(K-Means) (1) | 2022.12.05 |
| [기계학습/ML]13. 비지도학습 - 군집(Clustering) (0) | 2022.12.05 |
| [기계학습/ML]12. 앙상블 학습 - 랜덤 포레스트, 엑스트라 트리, 그레이디언트 부스팅 (0) | 2022.10.24 |
| [기계학습/ML]11. 검증 세트 - 교차 검증, 그리드 서치 (0) | 2022.10.24 |



